0 と 1 だけで話す種族
その国の種族は 0 と 1 だけで構成されたアルファベットを使って話しているとしよう。
ただ、0 と 1 をめちゃめちゃに並べて話してもお互いに意味は通じないから、意味のある言葉にするには、0 と 1 をある規則で並べて話す。
(ここに書いた文章だってそうなってる。日本語という言語の中からひとつひとつの文字を日本語の文法に則って並べてるから、僕の言葉はあなたに通じている。これから話を進める種族の言語体系は、日本語みたいに複雑で無数にある文字の組み合わせじゃなくて、もっともっと単純に 0 と 1 だけを文字として使っているというだけだ。)
さて、この種族の脳みその中を覗いてみよう。
彼らが「りんご」という意味の言葉を表すときに「001」という文字の並びを使うとする。
つまり話の中で「001」という並びに出会ったら、それを「りんご」と認識できるというわけだ。
言い換えれば、「りんご」を表すのは「001」という文字の並びに正規化されている文字列だってことだ。
(「正規化」ていうのは、つまり、文字の並び順が規則性を持って整えられてるってこと。)
オートマトンと正規表現
コンピュータが内部的には 0 と 1 だけでいろんなタスクを処理してるのは意外と有名な話だ。
コンピュータは {0,1} の国の種族にとっても似ている。
コンピュータに何か入力すると何でもかんでも 0 と 1 に翻訳して(置き換えて)から、彼らは仕事を始める。
つまり、正規化された 0 と 1 の並びを検索できる方法があれば、コンピュータは人間の言葉の中からあるパターンに当てはまる箇所を探し出してこれる。
これが所謂「正規表現」を使ったパターンマッチングって奴だ。
正規表現がパターンを認識するのに裏側で動いてる仕組みそのものを「有限オートマトン」と言ったりする。
決定性と非決定性
ここでは、オートマトンによる処理にいつかちゃんと終りがある有限オートマトンについて話を進める。
有限なオートマトンには2種類ある。
- 決定性有限オートマトン(DFA)
- 非決定性有限オートマトン(NFA)
の2つだ。
この記事の趣旨はこの2つの違いを Lisp のコードで追ってみて、理解しよう(この記事の後半を参照)ってことなんだけど、Lisp やプログラミング言語に慣れない人の為にざっくり話だけしてしまおう。
実際のオートマトンを表現した図を見てみよう。
(以下、全て図は 計算理論の基礎 [原著第2版] 1.オートマトンと言語 から転載)
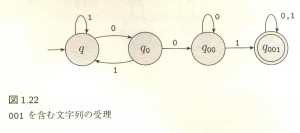
「001を含む文字列の受理」・・・ふむ。少し説明しよう。
まず用語的なところから。
図にある丸の部分を「ノード(接点、または節点)」、矢印を「エッジ(辺)」という習慣がある。
それから「受理(accept)」と言ったら、入力された文字列の中に目的のパターンを見付けられたよってことだ。
逆に「拒否(reject)」と言われたらパターンがマッチしなかったから出直して来い!という意味。
(極端に正規化されたお役所の仕事を思い出してくれれば理解しやすいと思う。同じ人間が仕事してるとは思えないことも多々あるよね!)
図の左端、左側にノードがないエッジが言葉の入力部分だ。ここにいろんな 0 と 1 の並びが入ってくる。
ノード:q は入力された文字列を受け取って振り分ける。
どう振り分けるかって言うと、文字列の最初が 1 だったら、もう一回自分自身に入力を戻して次の文字をチェックする。
文字列の最初が 0 だったら、目的の「001」にマッチする見込みがあるから、チェックし終わった1文字目(0)を除いた残りを次のノード:q0 に渡す。
これでノードとエッジの表記が何を意味しているかだいたいつかめただろうか?
各ノードは最初の文字をチェックしてOKだったらチェックしていない残りの文字列を次のノードに渡していく。
マッチが成功し続ければ最終的に右端の二重丸になってるノード:q001 にたどり着く。
二重丸は「受理(accept)」の意味だ。
ノード:q001 にたどり着いた時点で入力文字列にマッチする箇所(= “001”)があることは分かっているから、ノード:q001 は残りの文字列を単に自分自身に再入力しながら入力文字列が尽きるまで消化作業を続けて、文字列が空っぽになったところで終了する。
逆に、マッチする部分がどこにもなかった入力はどうなるか?
ノード:q からノード:q00 の間を行ったり来たりしてるうちに文字列が空っぽになってしまって受理(accept)されないまま処理が終了する。
つまり「拒否(reject)」ってことだ。
で、このタイプの有限オートマトンのことを決定性有限オートマトン(DFA)と呼んでる。
なんでか?
入力として与えられた文字列が順繰り一文字ずつ消化されながら、必ず(自分自身も含めた)各ノードのいずれかに引き継がれる。
処理は決定論的で、辿れる可能性のある「別の道」なんてものはない。
つまり一方通行で全ての処理が消化されるから「決定性」という言葉が似合うというわけだ。
じゃあ、「決定性」に対する「非決定性」ってなんなの?と思うだろう。
OK、まずは実際の図を見てみよう。
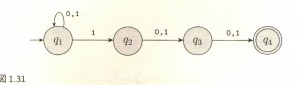
「先生!何が違うんですか!?」
いい質問だ。
まず初めに言っておかなきゃいけないのは、このオートマトンは最初に出てきた「りんご(= 001)」を受理するものとは別の「言葉」を認識する。
今回受理するのは「ケツから3番目が 1 である言葉」だ!
つまり「00100」は受理されるけど、「0010」は最後から3番目が 0 だから拒否される。
これを記号論的観点から「メロン」を見付けるオートマトンとでもしよう。
さて、では「りんご」と違って「メロン」はどの辺が「非決定」的なのか。
注目すべきはノード:q1 の仕事だ。
ノード:q1 は入力文字列の最初の文字が 0 でも 1 でも文字列の残りを自分自身に再入力する。
にも関わらずだ、入力文字列の最初の文字が 1 なら、残りをノード:q2 に渡してる。
どっちやねん!と思った人はちょっと落ち着いて、「選択の可能性」ってものを想像してみよう。
あなたは森のなかで道に迷っている。
ただでさえどっちに行ったらいいのか皆目検討がつかないのに分かれ道に出くわしたとしよう。
当てずっぽうに右へ行ってみようと思う。
でも右へ行った先が間違いだったら、またここに戻ってきて左へ行けるように何か目印を置いた上で右に進む(例えば貴重な食料の食パンを少しちぎって分岐点に置いておく)。
つまり複数の選択肢がある場合、ランダムに試してみて運良く受理されたらラッキー、運悪く拒否されたら目印まで戻ってやり直し、といくつかの道筋を試しながら正解を探す方法が思い浮かぶだろう。
図1.31 のオートマトンに話を戻そう。
ノード:q1 が受け取った文字列の最初が 0 だったら。
この場合、まずは 1 にマッチしなきゃいけないわけだから、その 0 を捨てて残りを自分に戻すのは的確な判断だ。
では受け取った文字列の最初が 1 だったら。
マッチの可能性はあるけど、このオートマトンが探してる 1 は「文字列の最後から3番目の 1」でなければならない。
なので、
- 見つけた 1 が目的の 1 (=文字列の最後から3番目の 1 )でない可能性もあるので、選択肢の一つとして自分に戻しておく。つまりパンくずを置く
- 見つけた 1 が目的の 1 であることに賭けて、思い切って文字列の残りをノード:q2 に渡す
という2つの道を探る。
もうお分かりだろう。この処理方法が組み込まれたオートマトンを「非決定性有限オートマトン(NFA)」と呼んでいる。
見分け方としては、一つのノードから複数のエッジが出ていて、エッジのラベルに記載された要素(ここでは 0 とか 1 とか)が2つ以上のエッジで重複していたら、それは NFA だ。
(あ、もう面倒なので、いちいち長い名前で言うのはやめて、DFA、NFA っていう簡単な呼び方に統一します。)
驚くべきことをひとつ紹介しよう。
「全ての NFA は必ず等価な DFA に書き換えることができる。」
なんと。
そして次の図を見てビビっていただきたい。
図1.31 の NFA を等価な DFA に書き直すとこんなことになってしまう。
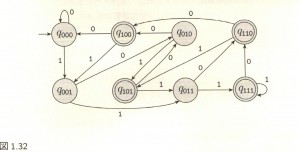
図1.31 でのノード:q1 における選択の自由を奪ってしまうと、こんなに複雑なオートマトンができあがる。
ただし、見た目はどんなに複雑でも、ある文字列を処理したとき、それを「メロン」として受理するか拒否するかという結果については等価だというのが驚きだ。
長々と解説してきたが、DFA と NFA の構造の違い、それと2つの等価性について少しでも理解していただけたら嬉しいと思う。
Lisp を使った実験
プログラマのために、DFA、NFA をそれぞれシュミレートした関数を載せておく。
言語は Common Lisp で書いている。
僕自身、学校で専門的な教育を受けたわけじゃないので「いや、こういうことでしょ?」という、言ってしまえばノリで書いてる部分が多分にある。
以下のコードがどこまで正確かは分からないが、オートマトンを理解する参考になってくれれば嬉しい。
ちなみに、以下のコードでは、メイン関数に与えられた引数が Null であった場合、また、0 と 1 以外の文字が含まれる文字列であった場合の例外処理などはことごとく省いている。
都合上、メイン関数に文字列を引数として与えた後、それを一文字ずつにバラした状態のリストを作り実際の処理を始めている。
alph_to_list.l
;; "001" -> '("0" "0" "1")
(defun alph->list (alph)
(cond ((string= alph "") '())
(t (loop for i upto (- (length alph) 1)
collect (subseq alph i (+ i 1))))))
DFA の再現

図1.22 を再掲した。
このオートマトンを正規表現で書き表わせば ‘^[01]*?001[01]*$’ となる。
平たく言えば、「001 を含む文字列にマッチする」ということだ。
001_DFA.l
;; match ^[01]*?001[01]*$
;; alph->list
(load "alph_to_list.l")
;; メイン関数
(defun call-DFA-*001* (alph)
(let ((lis (alph->list alph)))
(q-start lis)))
(defun q-start (lis)
(cond
((null lis) "reject")
((string= (car lis) "0") (q-0 (cdr lis)))
((string= (car lis) "1") (q-start (cdr lis)))))
(defun q-0 (lis)
(cond
((null lis) "reject")
((string= (car lis) "0") (q-00 (cdr lis)))
((string= (car lis) "1") (q-start (cdr lis)))))
(defun q-00 (lis)
(cond
((null lis) "reject")
((string= (car lis) "0") (q-00 (cdr lis)))
((string= (car lis) "1") (q-001 (cdr lis)))))
(defun q-001 (lis)
(cond
((null lis) "accept")
((string= (car lis) "0") (q-001 (cdr lis)))
((string= (car lis) "1") (q-001 (cdr lis)))))
見ての通り、繰り返しを全く気にせずに、各ノードの処理をバカ正直に書き下してみた。
理解を深めるきっかけという意味ではこの方が分かりやすいと思う。
決定論的な DFA では、各ノード内の処理は非常に単純になると同時に、どのノードも一様になることを確認していただければと思う。
実行結果
> (load "001_DFA.l") T > (call-DFA-*001* "001") "accept" > (call-DFA-*001* "0010") "accept" > (call-DFA-*001* "010") "reject"
NFA の再現

マッチパターンは ‘^[01]*?1[01]{2}$’
最後から3番目が 1 となる必要があるのでそこだけリテラルをそのまま置き、その後に続く [01]{2}$ で 0 または 1 からなるクラスに属する文字(つまり 0 か 1)が合計2文字続いて末尾に達すればマッチ成功である。
100_NFA.l
;; match ^[01]*?1[01]{2}$
(load "alph_to_list.l")
;; メイン関数
(defun call-NFA-*1.. (alph)
(let ((lis (alph->list alph)))
(q1 lis)))
(defparameter captcha '())
(defun restart-with-captcha ()
(q1 (cdr captcha)))
(defun q1 (lis)
(setf captcha lis) ;; ここが所謂、非決定性
(cond
((null lis) "reject")
((string= (car lis) "0") (restart-with-captcha))
((string= (car lis) "1") (q2 (cdr lis)))))
(defun q2 (lis)
(cond
((null lis)
(cond
((null captcha) "reject")
(t (restart-with-captcha))))
((or (string= (car lis) "0") (string= (car lis) "1"))
(q3 (cdr lis)))))
(defun q3 (lis)
(cond
((null lis)
(cond
((null captcha) "reject")
(t (restart-with-captcha))))
((or (string= (car lis) "0") (string= (car lis) "1"))
(q4 (cdr lis)))))
(defun q4 (lis)
(cond
((null lis) "accept")
(t (restart-with-captcha))))
一つ前の DFA をコード化したものに比べると、一見したところオートマトンの図からそのままトレースしたようには見えない部分もあるかと思う。
関数の中でやってることも少し複雑になっているし、何よりグローバルな変数(captcha)を用意して副作用を利用している。
変数名や関数名から想像していただきたい。
captcha は分かれ道に出くわした時点のキャプチャであり、この変数に格納されたその時点でのリストの姿がパンくず代わりとなる。
そしてマッチが失敗したと判ったら、restart-with-captcha が呼ばれて、分かれ道まで戻ってやり直す。
実行結果
> (load "100_NFA.l") T > (call-NFA-*1.. "00100") "accept" > (call-NFA-*1.. "00101") "accept" > (call-NFA-*1.. "00001") "reject"
NFA -> DFA

以下が 100_NFA.l を DFA に書き直したものだ。
さすがにここまでたくさんのノードを繰り返し(しかも中身の形式はいっしょ!)書くのは苦痛なので、マクロを定義してスッキリさせてある。
100_DFA.l
;; match ^[01]*?1[01]{2}$
(load "alph_to_list.l")
;; メイン関数
(defun call-DFA-*1.. (alph)
(let ((lis (alph->list alph)))
(q000 lis)))
(defmacro judge (lis result when-0 when-1)
`(cond
((null ,lis) ,result)
((string= (car ,lis) "0") (,when-0 (cdr lis)))
((string= (car ,lis) "1") (,when-1 (cdr lis)))))
(defun q000 (lis)
(judge lis "reject" q000 q001))
(defun q001 (lis)
(judge lis "reject" q010 q011))
(defun q010 (lis)
(judge lis "reject" q100 q101))
(defun q011 (lis)
(judge lis "reject" q110 q111))
(defun q100 (lis)
(judge lis "accept" q000 q001))
(defun q101 (lis)
(judge lis "accept" q010 q011))
(defun q110 (lis)
(judge lis "accept" q100 q101))
(defun q111 (lis)
(judge lis "accept" q110 q111))
コードの見た目はこんなに違うのに、NFA と全く同じく動作することを確かめてほしい。
実行結果
> (load "100_DFA.l") T > (call-DFA-*1.. "00100") "accept" > (call-DFA-*1.. "00101") "accept" > (call-DFA-*1.. "00001") "reject"
コラム
オートマトンの中身を理解することは、(プログラマなら)日常的に使っている正規表現エンジンの動きを理解することに繋がる。
参考: 正規表現が処理する順番、少し効率性について
プログラマでなくても、例えば会社組織の中でマネージャやプランナー的な仕事をしている人なら、タスクの動きを把握したり、より正確で効率的なワークフローを考えるのに役立つだろう(でもやり過ぎちゃいけない。最初のほうで述べたように「お役所仕事」になってしまっては本末転倒だ)。
正規化という概念は、実は誰でも日常的に用いている。
他の誰かに仕事を任せるとき、特にその仕事の成否が自分に返ってくる場合は、仕事の成果の「正しさ」が判断できる基準を設けるだろう。
大雑把に言えばこれこそ正規化だ。
本文で言っている「マッチする・しない」という表現は、この場合の「判断基準」に置き換えることができる。
判断基準には矛盾がなく、誰が見ても的確に評価できるものがよい。
そういう観点からすると、何をもって「正規」と言えるのか、その考え方の根本は誰しもが少しでも考えてみるべきだと思う。